FDP on Algebra, Analysis, and Number Theory Concluded Successfully
The Department of Mathematics at SRM University-AP hosted a successful Faculty Development Programme (FDP) on Algebra, Analysis, and Number Theory (AAN–2024) from December 16 to 20, 2024. This initiative aimed to strengthen faculty expertise in foundational mathematical disciplines essential for undergraduate (UG) and postgraduate (PG) education while also promoting effective teaching strategies.
Held online via Zoom, the programme attracted over 500 interested participants from across India, although due to platform capacity, 480 were accommodated. The FDP featured a series of keynote lectures by distinguished speakers focusing on core areas of mathematics.
Prof. V Kannan delivered an extensive session on analysis, discussing key theorems such as the Bolzano-Weierstrass theorem, the Intermediate Value Theorem, and the Heine-Borel theorem. The theoretical insights were complemented by tutorial sessions led by research scholars Mr Priti Prasanna Mondal and Ms Athulya P, who assisted participants in reinforcing their understanding through practical examples.
In the realm of number theory, Prof. Kalyan Chakraborty’s engaging lectures covered topics including plane curves, rational points, and elliptic curves, emphasising their importance and applications. Tutorial sessions by Dr Arkabrata Ghosh and research scholar Ms Leena Mondal supported these discussions with additional insights.
Dr Subha Sandeep Repaka presented comprehensive lectures on algebra, detailing concepts such as the structure of cyclic groups, Lagrange’s theorem, and Sylow’s theorems. These sessions were paired with tutorials that helped participants apply and solidify their knowledge.
Under the leadership of Convenor Dr Sandeep Kumar Verma and Co-Convenors Dr M Radhakrishnan and Dr G Damodar Reddy, the FDP offered valuable insights into advanced mathematical topics and innovative pedagogical approaches. Dr. Verma expressed gratitude for the overwhelming response, stating, “It was a privilege to organise this FDP, bringing together experts and participants to explore the depths of algebra, analysis, and number theory. This programme has served as a platform for knowledge exchange, fostering collaboration and growth in the field.”
The programme marked a significant step towards enhancing mathematics education and research, inspiring participants to incorporate new ideas and methodologies in their academic endeavours.
- Published in Departmental News, Math News, News
Prof. Mythily Ramaswamy on Exploring the Intersection of Fourier Analysis and Partial Differential Equations
 The Department of Mathematics hosted its 9th Distinguished Lecture, “PDE through Fourier” on September 18, 2024. The speaker, Prof. Mythily Ramaswamy, a renowned scholar in the fields of partial differential equations, control theory, and fluid dynamics addressed a crowd of faculty members, PhD students, MSc students, and attendees from various other Departments.
The Department of Mathematics hosted its 9th Distinguished Lecture, “PDE through Fourier” on September 18, 2024. The speaker, Prof. Mythily Ramaswamy, a renowned scholar in the fields of partial differential equations, control theory, and fluid dynamics addressed a crowd of faculty members, PhD students, MSc students, and attendees from various other Departments.
Prof. Mythily Ramaswamy’s lecture delved into the intricate development of partial differential equations (PDE) as influenced by the groundbreaking work on heat conduction by Fourier in the early 19th century. Prof. Ramaswamy, skillfully traced the history of Fourier’s discovery, leading to the formulation of the Fourier Series—a fundamental aspect of solving PDEs. She also explored modern developments in Fourier analysis and its vital applications in the realm of PDEs.
Prof. Mythily is currently serving as a NASI Senior Scientist at the International Centre for Theoretical Sciences (ICTS-TIFR) in Bengaluru, she has held significant positions such as Dean at the TIFR Centre for Applicable Mathematics. A recipient of the prestigious P C Mahalanobis Medal from the Indian National Science Academy, Prof. Ramaswamy is recognised for her substantial contributions to nonlinear functional analysis and optimal control, and she takes pride in mentoring the next generation of mathematicians.
Following the lecture, a lively 15-minute Q&A session provided attendees the opportunity to engage with Prof. Ramaswamy. Participants raised thoughtful questions, which sparked invigorating discussions on the applications of PDEs and the pivotal role of Fourier analysis in modern mathematics. The speaker’s valuable insights enriched the audience’s understanding and prompted further interest in the subject.
The event was deemed a resounding success, significantly enriching the academic experience of all participants. Both PhD students and faculty members gleaned crucial knowledge from Prof. Ramaswamy’s expertise, enhancing the intellectual atmosphere of the university. This lecture is poised to positively impact the institution’s academic reputation and foster future research collaborations. The Department of Mathematics looks forward to hosting more events that contribute to the vibrant academic community.
- Published in Departmental News, Math News, News
Prof. R Ramanujam Exploring the Role of Mathematics and Science in Social Inclusion
 On October 4, 2024, Department of Mathematics at SRM University-AP hosted its 10th Distinguished Lecture, featuring renowned mathematician and educator Prof. R Ramanujam. The event attracted a diverse audience, including BSc and BTech students, PhD candidates, and faculty members, all eager to engage with the critical topic of mathematics and science education for students from socially and economically marginalised backgrounds.
On October 4, 2024, Department of Mathematics at SRM University-AP hosted its 10th Distinguished Lecture, featuring renowned mathematician and educator Prof. R Ramanujam. The event attracted a diverse audience, including BSc and BTech students, PhD candidates, and faculty members, all eager to engage with the critical topic of mathematics and science education for students from socially and economically marginalised backgrounds.
Prof. Ramanujam’s lecture posed a thought-provoking question: “What do mathematics and science education mean to a student from socially and economically marginalised sections?” Drawing from his extensive experience in various educational contexts, he provided valuable insights into the intersection of education and social equity. His work with the Tamil Nadu Science Forum, government curriculum bodies, and teacher education programs at Azim Premji University in Bengaluru informed his perspective on the necessity of aligning educational practices with the realities faced by marginalised communities.
During his talk, Prof. Ramanujam emphasised the importance of conducting educational research that is deeply rooted in social contexts. He argued that curriculum-making decisions should be informed by such research to ensure that education is socially inclusive and responsive to the unique challenges faced by disadvantaged students. His advocacy for an education system that addresses the needs of all learners resonated strongly with the audience, highlighting the potential for education to serve as a transformative force in society.
Prof. R Ramanujam is a distinguished figure in the fields of mathematics and education. He completed his PhD at the Tata Institute of Fundamental Research (TIFR) and pursued postdoctoral work at the City University of New York (CUNY), USA. His long-standing association with the Institute of Mathematical Sciences (IMSc) in Chennai and his current role as a visiting professor at Azim Premji University further underscore his commitment to advancing educational practices.
The lecture provided a stimulating exploration of how mathematics and science education can help address social inequalities. Prof. Ramanujam’s reflections on education, grounded in his experiences with marginalised communities, left a lasting impact on attendees. The event concluded with an engaging Q&A session, where participants raised questions about the challenges of implementing socially rooted educational reforms. This discussion reinforced the lecture’s key themes of inclusivity and the transformative potential of education when designed to meet the diverse needs of learners.
The 10th Distinguished Lecture at SRM University-AP not only highlighted the importance of educational equity but also inspired dialogue on how institutions can better serve all students, particularly those from marginalized backgrounds.
- Published in Departmental News, Math News, News
Breakthrough in Mathematical Research: Dr Subha Sandeep Repaka’s Innovative Study on Unitary Groups

The Department of Mathematics, SRM University-AP, is pleased to announce that Assistant Professor Dr Subha Sandeep Repaka has published a significant research paper titled “On Reducibility of Induced Representations of Odd Unitary Groups: The Depth Zero Case.” This accomplishment reflects Dr Repaka’s expertise and dedication to advancing mathematical research, further enriching the academic contributions of the department and the university.
Abstract:
We study a problem concerning parabolic induction in certain $p$-adic unitary groups. More precisely, for $E/F$ a quadratic extension of $p$-adic fields the associated unitary group $G=\mathrm{U}(n,n+1)$ contains a parabolic subgroup $P$ with Levi component $L$ isomorphic to $\mathrm{GL}_n(E) \times \mathrm{U}_1(E)$. Let $\pi$ be an irreducible supercuspidal representation of $L$ of depth zero. We use Hecke algebra methods to determine when the parabolically induced representation $\iota_P^G \pi$ is reducible.
Future Research Plans:
We would like to solve the same problem which I had solved in this paper for the groups U(n,n) and U(n,n+1) over p-adic fields using L-Functions which is a very novel approach.
The link to the article:
http://nyjm.albany.edu/j/2024/30-50.html
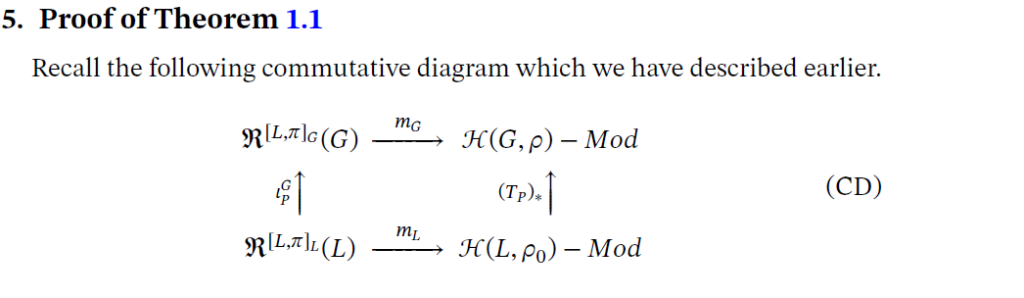
- Published in Departmental News, Math News, News, Research News
Dr Negi’s Research Exploration of the Sugeno Exponential Function and Its Multidisciplinary Applications

Dr Shekhar Singh Negi from the Department of Mathematics has published a research paper titled “A note on Sugeno exponential function with respect to distortion.” Dr Negi’s research investigates the Sugeno exponential function. This research develops new mathematical tools and rules to work with a different way of measuring things, which can be useful in various fields like economics, biology, or any area where traditional measurements don’t quite fit the problem at hand.
Abstract:
This study explores the Sugeno exponential function, which is the solution to a first order differential equation with respect to nonadditive measures, specifically distorted Lebesgue measures. We define k-distorted semigroup property of the Sugeno exponential function, introduce a new addition operation on a set of distortion functions, and discuss some related results. Furthermore, m-Bernoulli inequality, a more general inequality than the well-known Bernoulli inequality on the real line, is established for the Sugeno exponential function. Additionally, the above concept is extended to a system of differential equations with respect to the distorted Lebesgue measure which gives rise to the study of a matrix m-exponential function.
Finally, we present an appropriate m-distorted logarithm function and describe its behaviour when applied to various functions, such as the sum, product, quotient, etc., while maintaining basic algebraic structures. The results are illustrated throughout the paper with a variety of examples.
Collaborations:
Prof. Vicenc Torra, Professor at the Department of Computing Science at Umea University. His area of research include artificial intelligence, data privacy, approximate reasoning, and decision making.
Future Research Plans:
To explore the aforementioned derivative and investigate results with applications in real life.
- Published in Departmental News, Math News, News, Research News
Unraveling Chaos Dynamics in Cancer: Dr Koyel Chakravarty’s Breakthrough Research
 Dr Koyel Chakravarty, Assistant Professor in the Department of Mathematics, has made a significant contribution to the field of cancer research with her paper “Analysis and Regulation of Chaos Dynamics in a Cancer Model through Chemotherapeutic Intervention and Immune System Augmentation,” which was recently published in the International Journal of Dynamics and Control. In her paper, Dr Chakravarty delves into the intricate world of chaos dynamics within a cancer model and explores the potential for regulating these dynamics through the combined approach of chemotherapeutic intervention and immune system augmentation.
Dr Koyel Chakravarty, Assistant Professor in the Department of Mathematics, has made a significant contribution to the field of cancer research with her paper “Analysis and Regulation of Chaos Dynamics in a Cancer Model through Chemotherapeutic Intervention and Immune System Augmentation,” which was recently published in the International Journal of Dynamics and Control. In her paper, Dr Chakravarty delves into the intricate world of chaos dynamics within a cancer model and explores the potential for regulating these dynamics through the combined approach of chemotherapeutic intervention and immune system augmentation.
Her research offers insights into understanding the complex behaviour of cancer cells and how such insights can be leveraged to develop more effective treatment strategies. Dr Chakravarty’s work marks a crucial step forward in the ongoing efforts to combat cancer, shedding light on the dynamic interplay between therapeutic interventions and the body’s immune response.
The publication of this paper not only underscores Dr Koyel’s expertise in the field of mathematical analysis in cancer research but also signifies a promising advancement in the collective pursuit of understanding and addressing the challenges posed by cancer.
Abstract
The focus of the current investigation lies in the formulation and analysis of a dynamic model depicting cancer growth, incorporating the joint influences of chemotherapy and immune system augmentation. The primary emphasis of this study revolves around the analysis of the dynamic behaviour within a living-cell closed carcinoma system, specifically one devoid of external vitamin support, with a particular exploration of chaos dynamics. Subsequently, the authors aim to scrutinise the pivotal impact of infused vitamins in attaining stable system dynamics through the application of chaos control techniques.
The formulated model exhibits fundamental mathematical properties, revealing a spectrum of co-dimension one and co-dimension two bifurcations. The identification of specific bifurcation types relies on algebraic criteria techniques, where conditions necessary and sufficient for bifurcation types are developed. Notably, these criteria are distinct from traditional approaches based on the characteristics of the eigenvalues of the Jacobian matrix, instead relying on coefficients derived from characteristic equations. The accuracy of the analytical conclusions is validated through numerical findings, elucidating diverse bifurcation structures. The article enriches its contribution by delving into the control of chaos through the reinforcement of the internal immune system and the maintenance of the biological system’s stability. This work culminates in proposing future directions aimed at advancing a more realistic approach to eradicating cancer.
Research in Layperson’s Terms
This study focuses on developing and analysing a model that simulates how cancer grows, considering both chemotherapy and the immune system’s response. The main goal is to understand how cancer behaves over time in a system that doesn’t have external vitamin support, especially looking at how chaotic or unpredictable the growth can become. The researchers also investigate how adding vitamins might help stabilise this chaotic system using specific control techniques. The model they created has certain mathematical features that show different types of changes, called bifurcations, which can occur under specific conditions.
Additionally, the study explores how strengthening the immune system might help control this chaos and stabilise the biological system. The paper concludes by suggesting future research directions that could lead to more effective cancer treatment strategies.
Practical implementation
The practical implementation and social implications of analysing and regulating chaos dynamics in a cancer model through chemotherapeutic intervention and immune system augmentation can be profound. Insights gained from this research could be applied to optimize cancer treatment protocols, potentially leading to more effective therapies with reduced side effects. By understanding and controlling the chaotic behaviour in cancer systems, patient outcomes could be improved through personalized treatment strategies.
Socially, the adoption of these findings may lead to increased public confidence in advanced cancer treatments, as well as a broader acceptance of integrating immune system support with traditional therapies. The potential for more stable and predictable treatment outcomes may also reduce the emotional and financial burden on patients and healthcare systems. Additionally, this approach may encourage further interdisciplinary research, bridging gaps between Mathematics, Biology, and Medicine, thus fostering innovation in cancer therapy development.
Collaborations
Dr Lakshmi Narayan Guin, Associate Professor, Department of Mathematics, Siksha Bhavana, Visva-Bharati
Future research plans
Potential areas for further exploration include:
- Personalised Medicine: Developing patient-specific models that consider individual biological variations could lead to more tailored and effective cancer treatments, minimising side effects and improving outcomes.
- Integration with Advanced Therapies: Combining the insights from chaos dynamics with emerging therapies such as immunotherapy, targeted therapy, and gene editing could enhance the precision and efficacy of cancer treatments.
- Published in Departmental News, Math News, News, Research News
Chetna: Awakening Mathematical Minds
 The Department of Mathematics at SRM University-AP successfully conducted a two-week summer programme “Chetna: Awakening Mathematical Minds” from June 17th to June 28th, 2024. This programme aimed to inspire and enhance mathematical understanding among participants from various parts of the country. The programme saw enthusiastic participation from 25 students hailing from different states across India, including West Bengal, Assam, Kerala, Karnataka, Tamil Nadu, Maharashtra, Gujarat, Delhi and Andhra Pradesh.
The Department of Mathematics at SRM University-AP successfully conducted a two-week summer programme “Chetna: Awakening Mathematical Minds” from June 17th to June 28th, 2024. This programme aimed to inspire and enhance mathematical understanding among participants from various parts of the country. The programme saw enthusiastic participation from 25 students hailing from different states across India, including West Bengal, Assam, Kerala, Karnataka, Tamil Nadu, Maharashtra, Gujarat, Delhi and Andhra Pradesh.
The programme featured a diverse curriculum, covering a wide range of mathematical topics. Eleven subjects were taught by eleven distinguished faculty members from the Department of Mathematics. The subjects provided a broad and enriching mathematical experience, designed to ignite a passion for mathematics in the participants.
Insights of the Two-Week Programme
First Week Highlights
1. Number Theory by Prof. Kalyan Chakraborty
The first week began with an in-depth exploration of Number Theory. Prof. Kalyan Chakraborty introduced participants to fundamental concepts such as divisibility, prime numbers, and modular arithmetic. The engaging sessions provided a strong foundation in understanding the properties and applications of numbers.
2. Abstract Algebra by Dr Anirban Bose
Dr Anirban Bose led the sessions on Abstract Algebra, diving into structures like groups, rings, and fields. The course covered essential algebraic concepts and their applications, enhancing the participants’ problem-solving skills and theoretical knowledge.
3. Linear Algebra and Basic Operators by Dr Animesh Bhandari
Dr Animesh’s lectures on Linear Algebra included topics such as vector spaces, linear transformations, and matrices. The sessions aimed to build a solid understanding of linear systems and the role of operators in mathematical computations.
4. Graph Theory by Dr Fouzul Atik
Graph Theory, taught by Dr Fouzul Atik, introduced participants to the study of graphs, which are mathematical structures used to model pairwise relations between objects. Topics included graph traversal, connectivity, and graph colouring, providing insights into the practical applications of graph theory.
5. Ordinary Differential Equation by Dr Nityananda Roy
The week concluded with Dr Nityananda Roy’s sessions on Ordinary Differential Equations (ODEs). This course covered methods of solving first-order and higher-order ODEs, along with real-world applications of differential equations in various fields.
Second Week Highlights
1. Advanced Algebra by Dr Kalyan Banerjee
Building on the first week, this subject delved deeper into algebraic structures, including advanced group theory and ring theory, preparing students for research-level problems.
2. Metric Spaces by Dr Choiti Bandyopadhyay
Dr Choiti’s sessions on Metric Spaces introduced participants to the concepts of distance and convergence in metric spaces. Topics included open and closed sets, continuity, and compactness, providing a deeper understanding of analysis.
3. Foundations of Probability and Statistics by Dr Vijayakrishna Rowthu
Dr. Vijayakrishna covered the Foundations of Probability and Statistics, focusing on probability theory, random variables, and statistical inference. The course aimed to equip participants with the skills needed to analyze and interpret data.
4. Mathematical Modelling by Dr Tapan Kumar Hota
Dr. Tapan’s lectures on Mathematical Modelling demonstrated how mathematics can be used to represent, analyse, and solve real-world problems. The course included case studies and practical applications in various disciplines.
5. Partial Differential Equation by Dr Ram Baran Verma
The sessions on Partial Differential Equations (PDEs) by Dr Ram Baran explored methods of solving PDEs and their applications in physics and engineering. Topics included separation of variables, Fourier series, and boundary value problems.
6. Math Education by Dr Jayasree Subramanian
The final course on Math Education, taught by Dr Jayasree, focused on pedagogical approaches and techniques for teaching mathematics effectively. The sessions aimed to inspire future educators and enhance their teaching methodologies.
Conclusion
The “Chetna: Awakening Mathematical Minds” summer programme was a resounding success, providing participants with valuable insights and knowledge in mathematics. The diverse backgrounds of the participants and the expertise of the faculty created a vibrant and stimulating learning environment, fostering a deeper appreciation for the subject. The Department of Mathematics at SRM University -AP looks forward to organising similar programmes in the future to continue inspiring young mathematical minds across the country.
- Published in Departmental News, Math News, News
Unlocking Cholesterol Homeostasis: A Mathematical Modelling Perspective
 In a significant stride towards understanding cholesterol homeostasis, Dr Koyel Chakravarty, Assistant Professor and Mr Sukdeb Manna, a PhD Scholar in the Department of Mathematics has co-authored a paper titled “Unlocking Cholesterol Homeostasis: A Mathematical Modelling Perspective.” The paper has been published in the esteemed journal, The European Physical Journal Plus, with an impact factor of 3.4. This collaborative effort showcases the innovative application of mathematical modelling in unravelling the complexities of cholesterol regulation within the body.
In a significant stride towards understanding cholesterol homeostasis, Dr Koyel Chakravarty, Assistant Professor and Mr Sukdeb Manna, a PhD Scholar in the Department of Mathematics has co-authored a paper titled “Unlocking Cholesterol Homeostasis: A Mathematical Modelling Perspective.” The paper has been published in the esteemed journal, The European Physical Journal Plus, with an impact factor of 3.4. This collaborative effort showcases the innovative application of mathematical modelling in unravelling the complexities of cholesterol regulation within the body.
The research not only contributes to the existing body of knowledge in this field but also sheds light on potential avenues for further exploration and understanding. Dr Chakravarty and Mr. Manna’s work underscores the importance of interdisciplinary approaches in scientific research and highlights SRM University-AP’s commitment to fostering cutting-edge research and innovation.
Their collaborative efforts serve as an inspiration to aspiring researchers and underscore the university’s dedication to pushing the boundaries of knowledge and discovery. Congratulations to Dr Chakravarty and Mr Manna on this remarkable achievement, and we look forward to more groundbreaking contributions from them in the future.
Abstract:
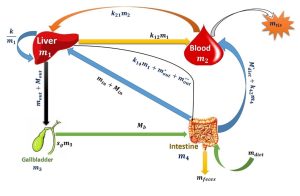
Limited progress in the mathematical modelling of cholesterol transport systems is hampering novel therapeutic interventions. This issue is addressed by the present study through precise design, employing four compartmental models to elucidate cholesterol dynamics in the comprehensive bloodstream. Disparities in medical advancements, particularly in cholesterol-related pathophysiology, are aimed to be bridged, advancing medical science and patient care outcomes.
Therapeutic strategies for reducing blood cholesterol are explored by the model, with parameter influences on equilibrium stability revealed through sensitivity analysis. System parameters are effectively manipulated by imposing sensitivity analysis, and pinpointing areas for model refinement. Stability analysis contributes to diverse realistic models, confirming local asymptotic stability. Model efficacy in studying cholesterol transport dynamics is supported by analytical and numerical assessments. The study concludes with the present model validation to substantiate it by comparing the present outcomes with the existing ones.
Explanation of The Research in Layperson’s Terms:
Basically, scientists are having trouble figuring out how to model how cholesterol moves around in the body, which is important for developing new treatments. This study tries to solve that problem by creating detailed models that show how cholesterol behaves in different parts of the bloodstream. The goal is to bridge the gap in medical knowledge about cholesterol-related problems and improve how we treat patients. The models help us understand how different treatments might affect cholesterol levels, and by analyzing them closely, we can figure out which factors are most important. This lets us tweak the models to make them more accurate. The study shows that the models are reliable by testing them both analytically and numerically, and comparing the results to what we already know.
Practical Implementation or the Social Implications of the Research
1. Personalized Medicine: The mathematical models developed in this research could help in designing personalized treatment plans for individuals with high cholesterol levels. By understanding how different factors affect cholesterol dynamics, doctors can tailor therapies to each patient’s specific needs, leading to more effective and targeted treatments.
2. Drug Development: Pharmaceutical companies could use these models to screen potential drugs for lowering cholesterol. By simulating how different compounds interact with cholesterol transport systems, researchers can identify promising candidates for further testing, potentially speeding up the drug development process.
3. Healthcare Cost Reduction: Better understanding of cholesterol dynamics could lead to more efficient use of healthcare resources. By optimizing treatment strategies and preventing complications related to high cholesterol, healthcare costs associated with conditions like heart disease could be reduced, benefiting both individuals and society.
4. Public Health Initiatives: Insights from the research could inform public health initiatives aimed at reducing cholesterol-related diseases. For example, policymakers could use the models to design targeted interventions such as education campaigns promoting healthy lifestyle choices or policies to improve access to cholesterol-lowering medications.
5. Improved Patient Outcomes: Ultimately, the goal of this research is to improve patient outcomes by better understanding and managing cholesterol homeostasis. By developing more accurate models of cholesterol transport dynamics, healthcare providers can make more informed decisions, leading to better control of cholesterol levels and reduced risk of cardiovascular disease and other related conditions.
Future Research Plans:
1. Current models may focus on a limited set of factors influencing cholesterol transport. Future research could explore the integration of additional biological factors such as genetic variations, hormonal influences, and dietary components into the models to create a more comprehensive understanding of cholesterol homeostasis.
2. Most existing models of cholesterol transport assume static conditions. Future research could develop dynamic models that capture the time-dependent changes in cholesterol levels in response to various stimuli, such as meals, physical activity, and medication intake. Dynamic models would provide a more accurate representation of real-world cholesterol dynamics and enable the evaluation of time-sensitive interventions.
Picture Related to the Research
- Published in Departmental News, Math News, News, Research News
Groundbreaking Mathematical Model Sheds Light on Bone Remodeling
 In a significant academic achievement, the Department of Mathematics is proud to announce that Dr Koyel Chakravarty, an Assistant Professor, along with her diligent PhD Scholar, Ms Amrutha Sreekumar, has made a remarkable contribution to the field of biological mathematics. Their paper, titled “Exploring the Impact of PTH Therapy on Bone Remodeling: A Mathematical Investigation,” has been officially accepted for publication in the prestigious Journal of Biological Systems by World Scientific.
In a significant academic achievement, the Department of Mathematics is proud to announce that Dr Koyel Chakravarty, an Assistant Professor, along with her diligent PhD Scholar, Ms Amrutha Sreekumar, has made a remarkable contribution to the field of biological mathematics. Their paper, titled “Exploring the Impact of PTH Therapy on Bone Remodeling: A Mathematical Investigation,” has been officially accepted for publication in the prestigious Journal of Biological Systems by World Scientific.
This paper presents a comprehensive mathematical model that investigates the effects of Parathyroid Hormone (PTH) therapy on bone remodelling processes. The research provides valuable insights that could potentially lead to more effective treatments for bone-related diseases and conditions.
The university community extends its heartfelt congratulations to Dr Chakravarty and Ms Sreekumar for their dedication and hard work.
Abstract
The regulatory role of parathyroid hormone (PTH) on bone, a crucial calcium reservoir, is influenced by sex steroids, notably estrogen. A mathematical model elucidates PTH-mediated bone remodeling mechanisms, examining plasma PTH effects and external dosages. Daily PTH injections, with their dual anabolic or catabolic action, offer a notable treatment for severe osteoporosis. This study predicts osteogenic responses to PTH, integrating factors like TGF-β, RANKL, and bisphosphonates in osteoblast-osteoclast signaling, alongside PTH’s effects on glands and regulatory molecules like Runx2, pCREB, and Bcl2. Using various methods, including simulations and sensitivity analysis, it aims to understand PTH therapy’s impact on bone volume, enhancing its clinical relevance.
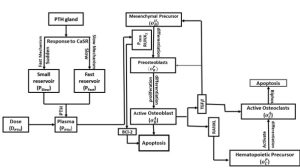
Explanation of the Research in Layperson’s Terms
The role of parathyroid hormone (PTH) in calcium storage within bones is significant, with its regulation influenced by other hormones, notably estrogen. A mathematical model has been developed to comprehend the effects of PTH on bones, examining both endogenous levels in the blood and exogenous intake requirements. It has been observed that daily PTH injections can be beneficial in treating severe bone conditions like osteoporosis, as these injections can induce either bone formation or resorption, depending on their administration method. Additionally, the response of bones to PTH is under scrutiny in this study, considering various substances such as TGF-β, RANKL, and bisphosphonates, and their interplay in maintaining bone health. Through the utilization of different methodologies including computer simulations, efforts are being made to precisely understand how PTH injections influence bone health, thereby enhancing their efficacy in addressing bone-related ailments.
Title of the Research paper in the Citation Format
Exploring the Impact of PTH Therapy on Bone Remodeling: A Mathematical Investigation
Practical Implementation or the Social Implications Associated
Personalized Treatment Plans:
Mathematical modeling of bone remodeling can facilitate the development of personalized treatment plans for individuals with bone disorders such as osteoporosis. By considering factors like hormone levels, genetic predispositions, and lifestyle factors, healthcare providers can tailor treatment strategies to optimize bone health outcomes.
1. Drug Development:
Insights gained from mathematical models can aid in the development of new drugs for bone disorders. By simulating the effects of potential therapeutic agents on bone remodeling processes, researchers can identify promising candidates for further investigation, potentially accelerating the drug discovery process.
2. Improved Clinical Decision Making:
Healthcare professionals can use mathematical models to make more informed clinical decisions regarding the management of bone disorders. By integrating patient-specific data into predictive models, clinicians can better predict treatment outcomes and adjust therapeutic interventions accordingly.
3. Enhanced Surgical Planning:
Mathematical modeling can also be valuable in surgical planning for procedures such as bone grafting or joint replacement. By simulating the effects of surgical interventions on bone remodeling, surgeons can optimize surgical techniques to promote more effective healing and long-term outcomes for patients.
4. Public Health Interventions:
Understanding the factors influencing bone remodeling at a population level can inform public health interventions aimed at reducing the burden of bone disorders. By identifying modifiable risk factors and developing targeted prevention strategies, policymakers can promote bone health and reduce the incidence of conditions like osteoporosis on a larger scale.
5. Educational Tools:
Mathematical models of bone remodeling can serve as educational tools for healthcare professionals, students, and patients. By visualizing complex biological processes in a simplified manner, these models can enhance understanding of bone physiology and the mechanisms underlying bone disorders, ultimately improving patient care and outcomes.
Collaborators:
• Prof. D.C. Dalal, Professor, Department of Mathematics, IIT Guwahati
• Dr. L.N. Guin, Associate Professor, Department of Mathematics, Visva-Bharati
Future research plans.
a) Incorporating Multi-Scale Modeling: Future research could focus on integrating multi-scale modeling approaches to capture the intricate interactions occurring at different levels of bone structure, from the molecular to the tissue level. By incorporating information on cellular processes, tissue mechanics, and systemic factors, these models could provide a more comprehensive understanding of bone remodeling dynamics.
b) Accounting for Heterogeneity: There is a need to develop mathematical models that account for the heterogeneity observed in bone remodeling processes across individuals and within different anatomical sites. By considering factors such as age, sex, genetics, and bone quality, researchers can create more personalized and accurate models to predict individual responses to treatment and disease progression.
c) Integration of Advanced Imaging Techniques: Advances in imaging technologies such as micro-computed tomography (micro-CT) and magnetic resonance imaging (MRI) provide detailed insights into bone structure and function. Future research could focus on integrating data from these advanced imaging techniques into mathematical models to enhance their predictive capabilities and enable non-invasive monitoring of bone remodeling in clinical settings.
d) Exploring Therapeutic Interventions: Researchers could use mathematical modeling to explore the efficacy of novel therapeutic interventions for bone disorders, such as drug treatments, exercise regimens, and dietary interventions. By simulating the effects of these interventions on bone remodeling processes, researchers can identify optimal treatment strategies and accelerate the development of new therapies.
Link to the article
- Published in Departmental News, Events, Math News, Research News
Celebrating Women’s Achievements in Pure and Applied Mathematics

The Department of Mathematics had organised an International Conference on Women in Pure and Applied Mathematics (WPAM). The five-day-long conference featured luminaries in the field of Mathematics and was funded by three prominent Indian government research bodies: SERB, NBHM, and CSIR.
The event saw Prof. Raman Parimala, a renowned Indian Mathematician, acclaimed for her contributions to the field of Algebra. The Conference was held with the purpose of providing an empathetic platform for women mathematicians to present their cutting-edge research work and to share their concerns about the gender gap in mathematical science.
Prof. Sanoli Gun (President of Asian Oceanian Women in Mathematics), Prof. Vijaylaxmi Trivedi (Chairperson, Indian Women in Mathematics), and Prof. Anisa Chorwadwala (Member, Indian Women in Mathematics) motivated the students and provided the students with valuable inputs on how to pursue their career further in Mathematics. The luminaries also discussed activities conducted by their organisations to encourage established women researchers, women PhD scholars and advanced undergraduate-level women students in Mathematics.
During the conference, activities such as poster presentations were held to facilitate mathematical interaction between students. The conference ended with the hope that there will be more opportunities to organise similar events.
- Published in Departmental News, Math News, News
























